今回は「機械装置の評価と分析/標準偏差と正規分布で確率を求める」についての記事です。
機械装置を組立てて試運転して評価するためには、数値で判断することが欠かせませんよね。気分や感情で「これでOK」などといったノリで決めるのではなく、データ測定して集めたデータを分析して判断するべきでしょう。
そこで今回の記事では、機械装置の部品や組立の精度と性能の評価をするために私が行っている分析方法を紹介しようと思います。
記事の目次
機械装置の評価と分析
機械装置の評価の必要性
「ものづくり」には「ばらつき」がつきものです。
これを聞いて皆さんはどう思われますか?
そもそも「ばらつきってなに?」って話しなんですが、私が言っているばらつきとはコレです。
-
目標値や設計値などの基準となる値と実際の値との差
これって「出来上がったもの」の見た目や実用に問題なければ気にすることではないのですが、私のように世に出回る製品を作る元となる機械装置を組立てていると、とても気になることなんです。

具体的にどんな場面でばらつきが気になるのか?と言いますと、この3つです。
-
部品の精度
-
組立の精度
-
組立てた機械装置の性能(生産される製品の精度)
機械装置の部品単品の精度が同じ部品なのに精度が同じではなかったり、組立の精度を数回測定すると毎回同じ数値にならなかったりするのです。そしてそのような状況で組立てた機械装置を動かして製品を作ってみると、製品の寸法に個体差がありバラバラなんです。そりゃそうなるわけなんですよね、部品単体の精度も組立の精度もばらつきがあれば、出来上がった機械装置の性能もばらつくのに決まっています。
そもそも、なんでこのような「ばらつき」が起きてしまうか?その原因にはこんなことが考えられます。
-
材料の差
-
機械の差
-
製造方法の差
-
検査方法の差
-
人のスキルによる差
参考
*測定の不確かさについてはこちらの記事をご覧ください
-

-
測定値のばらつきや矛盾は測定の不確かさにある【考え方の基本】
今回は「測定値のばらつきや矛盾は測定の不確かさにある」についての記事です。 私は機械組立の作業として、日常 ...
続きを見る
今回は詳しく掘り下げませんがこのようなことが原因でばらつきがおきてしまい、そして「ばらつきを0にすることはできない」のです。
でも、そんなことを言っていては、精度の保証も機械の性能の証明もできないわけで、それでは困ってしまいますよね。
そこで重要になることがコレです
-
どれくらいばらつくのか?を分析して評価する
ばらつくことを前提として、ばらつきを統計学に基づいたデータ分析をおこなうことで、「良否の判定」と「性能の証明」をすることができるようになります。
データ分析のポイント
私が何かを測定して「良否の判定」や「性能の証明」をするときのポイントは2つあります。

ポイント①
データの数
-
データは最低30回分測定する(N=30)
データの分析は、数値と数値を比べることなので「サンプルとなるデータ=サンプルサイズ=N数」が多ければ多いほどデータ分析の正確性が増しますが、正直サンプルデータの測定には時間もお金もかかります。
だから、沢山のデータ測定は大変なので一般的には最低30回分のサンプルがあればOKとしています。
*詳しくはこちらのブログで解説されています。 ⇒ 「標準偏差に必要なサンプルサイズはいくらか?」
ポイント②
分析は下記の5つを使っています(私の場合)
-
最小値・・・集めたデータの一番小さな値
-
最大値・・・集めたデータの一番大きいな値
-
平均値・・・データのばらつきの中心となる値。平均の表記は「μ」
-
標準偏差・・・データの偏りの程度を計るための指標となる値。標準偏差の表記は「σ」
- 正規分布(標準正規分布)・・・平均値を基準にして前後にどれくらいばらついているか?のグラフ
**詳しくは記事の後半で説明します。
これらを総合的に判断して、おかしな所がないか?修正すべき部分はないか?を判断しています。
データ分析の注意点は一峰性
データを集めて分析する前に、とても重要で注意しなけれなならないことがあるので紹介しておきます。
統計のデータで注意することはコレです
-
集めたデータをヒストグラムにしたとき一峰性であること
*ヒストグラムとは、値を分類や階級ごとに区分けして集計しグラフ化すること
一峰性のヒストグラム
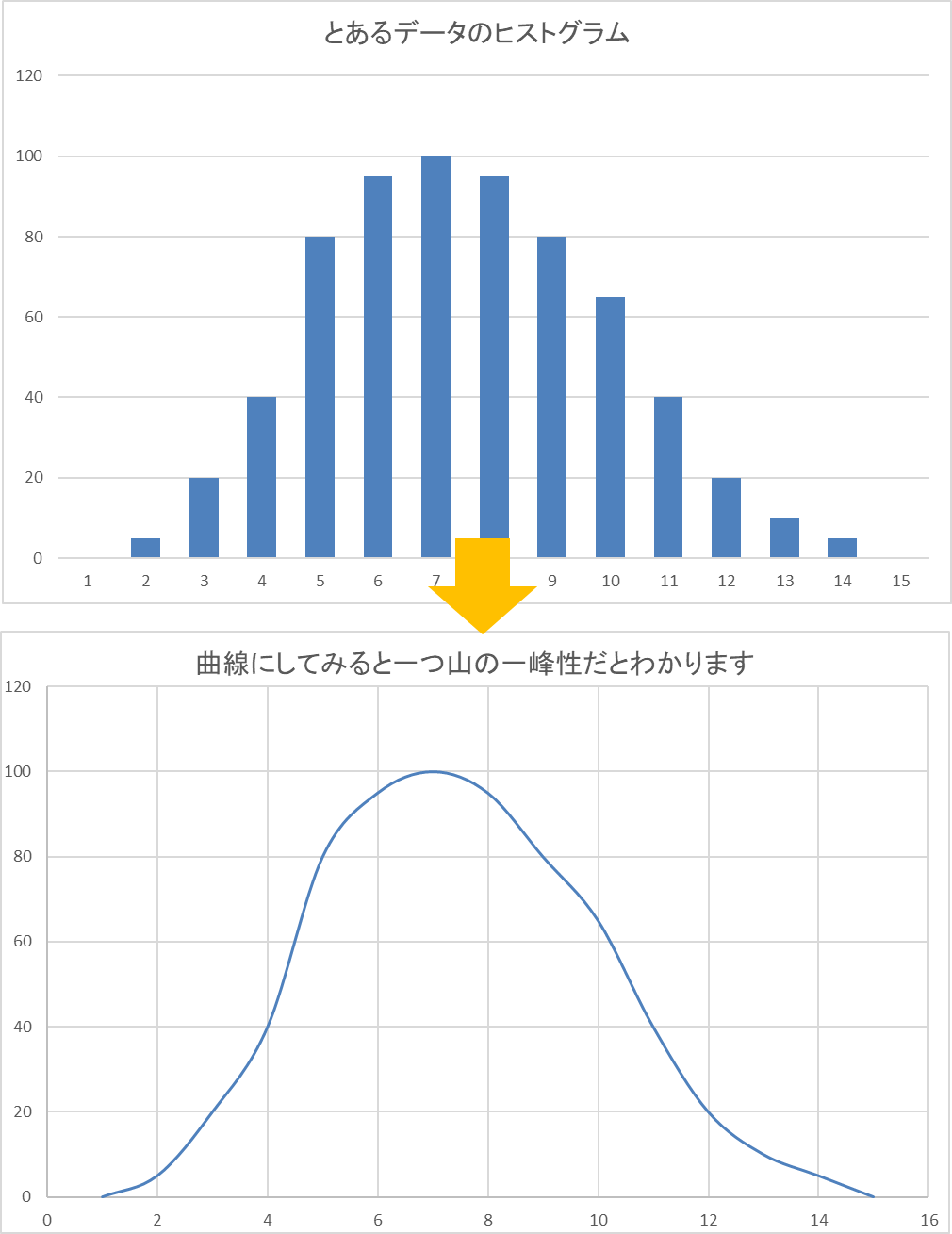
もし、ヒストグラムにしたときに山が一つの山の一峰性ではなく2つ山の二峰性や3つ山の三峰山の場合はこうなります。
-
「誤った集計によるデータ」や「間違ったデータが混ざっている」可能性がある
二峰性のヒストグラム
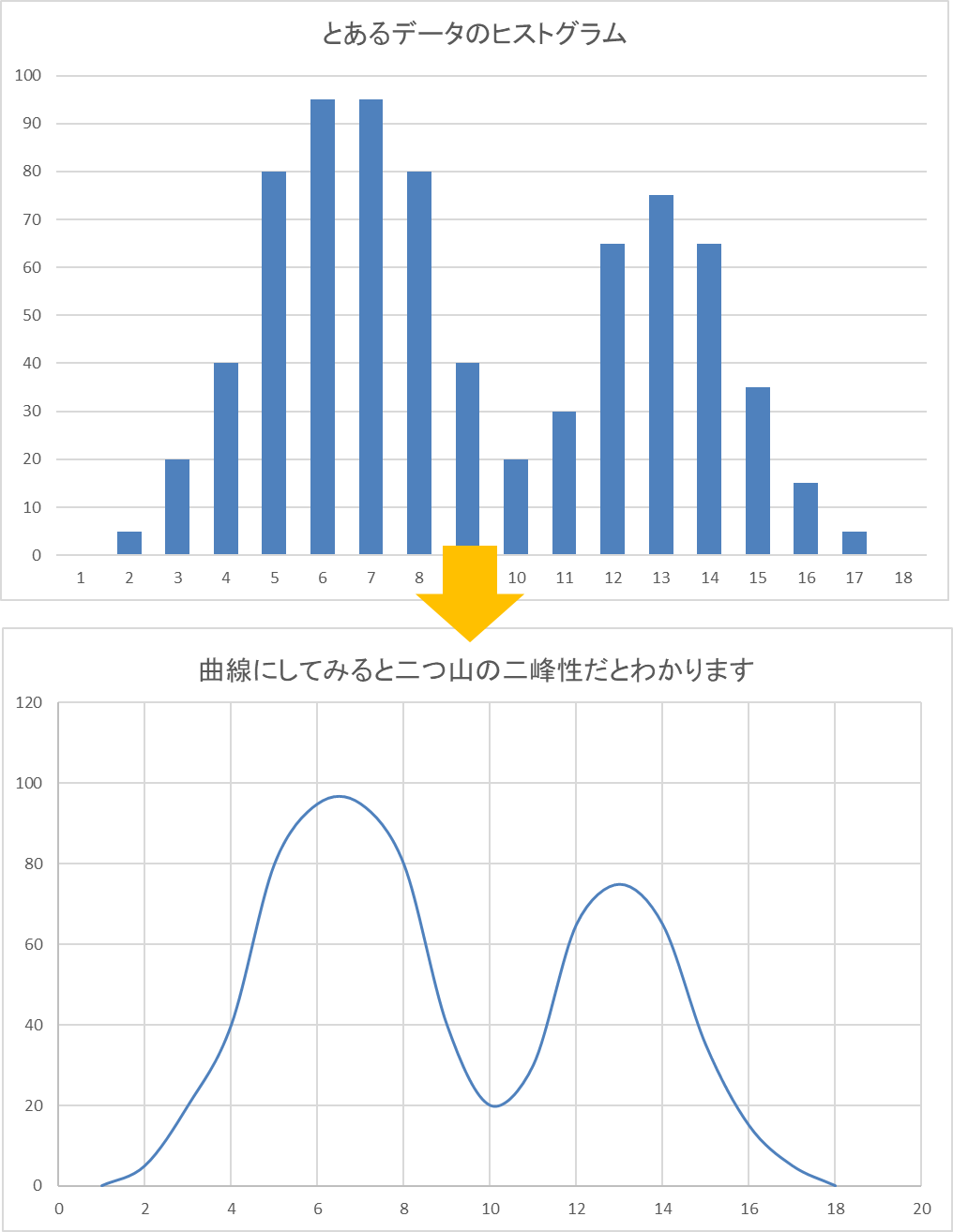
例えば上記の二峰性のデータで平均を求めたとしたらどうでしょうか?おそらく、グラフの谷から左にズレたあたりが平均値になるのですが、でもそれは本当に平均値と言えるのでしょうか?
このように、二峰性や三峰性のデータで分析すると誤った結果となってしまうので、正確な分析をするためには一峰性のデータが基本となるのです。
最小値と最大値と平均値と標準偏差と正規分布で評価する
測定データの分析例
下記のエクセルデータをご覧ください。
これは参考ですが、10回分の測定データを使って数値を分析しているものです。
例えばこんな感じのデータ
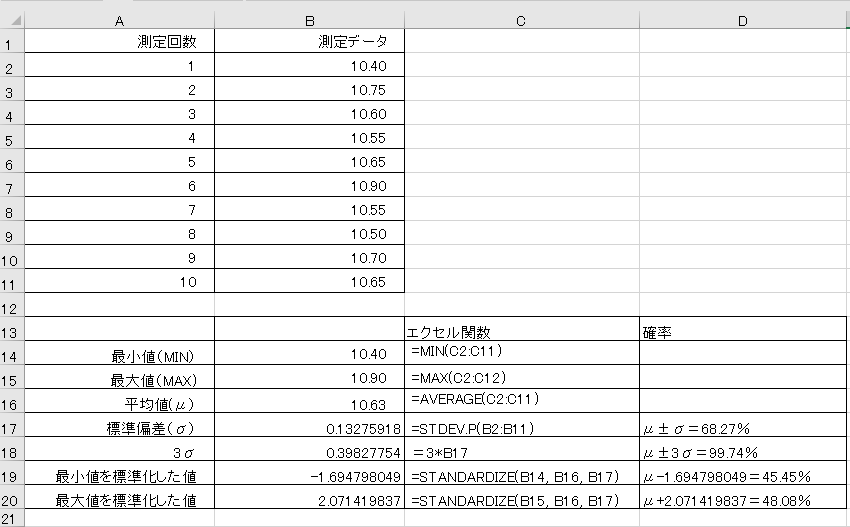
このように、測定したデータがどれくらいばらつくのか?を評価するために私が行っている方法は、最小値、最大値、平均値、標準偏差、正規分布を活用する方法です。
それではもう少し掘り下げて説明していきましょう。
最小値と最大値の活用
最小値と最大値のエクセル関数はコレです
-
=MIN(範囲) ・・・最小値
-
=MAX(範囲) ・・・最大値
最小値と最大値は計算する必要がないので、早い段階で異変に気付かせてくれます。
例えば、最小値/最大値が小さければばらつきが少なくて精度が高いと予想が付きますが、大きい値の場合は「異変がある」「精度が著しく悪いところがある」と分かるので早々に修正が必要だと判断ができます。
平均値(μ)の活用
平均値(μ)のエクセル関数はコレです
-
=AVERAGE(範囲) ・・・平均値
平均値はばらつきの中心(表記はμ)となる値で、基準値や目標値に対してプラス側とマイナス側のどちらに偏っているか?の判断をしたり、正規分布でデータがどれくらいばらついているのか?を判断するときの基準となる値です。
標準偏差(σ)の活用
標準偏差(σ)を求めるエクセル関数は下記の2通りです。
-
=STDEV.P(数値 1,[数値 2],...) ・・・データが全部そろっていればこの関数を使う。指定した値からばらつきを求める
-
=STDEV.S(数値 1,[数値 2],...) ・・・データが全部そろっていない場合はこの関数を使う。指定した値から予測でばらつきを求める
標準偏差はデータの偏りの程度を計るための指標となる値で、データ集計するときによく耳にする「シグマ値=σ値」とはこのことです。
標準偏差の活用方法は2つあります。
活用方法1 ±3σ
製造業で製品の良否の判断をするときに使われる±3σの条件に使う
製品の良否判断の条件とはコレです
-
基準に対して±3σは良品
-
μ(平均値)に対して±3σは良品
集めたデータから標準偏差=σを求めて、「3×σ=3σ」を基準や平均値の条件に照らし合わせて判断します。
活用方法2 正規分布と確率
標準偏差(σ)は正規分布に当てはめることでばらつきの程度やばらつきの確率が判断できます。
*正規分布(標準正規分布)でも説明します。
下記は正規分布のグラフですが、このグラフの面積を100としたときに集めたデータの分布の割合がどのくらいなのか?と言うことが分かります。
-
μ(平均値)±σ(標準偏差)の範囲に集めたデータの68.27%が含まれている
-
μ(平均値)±2σ(標準偏差)の範囲に集めたデータの94.45%が含まれている
-
μ(平均値)±3σ(標準偏差)の範囲に集めたデータの99.73%が含まれている
標準偏差が分かればばらつきの確率がわかります
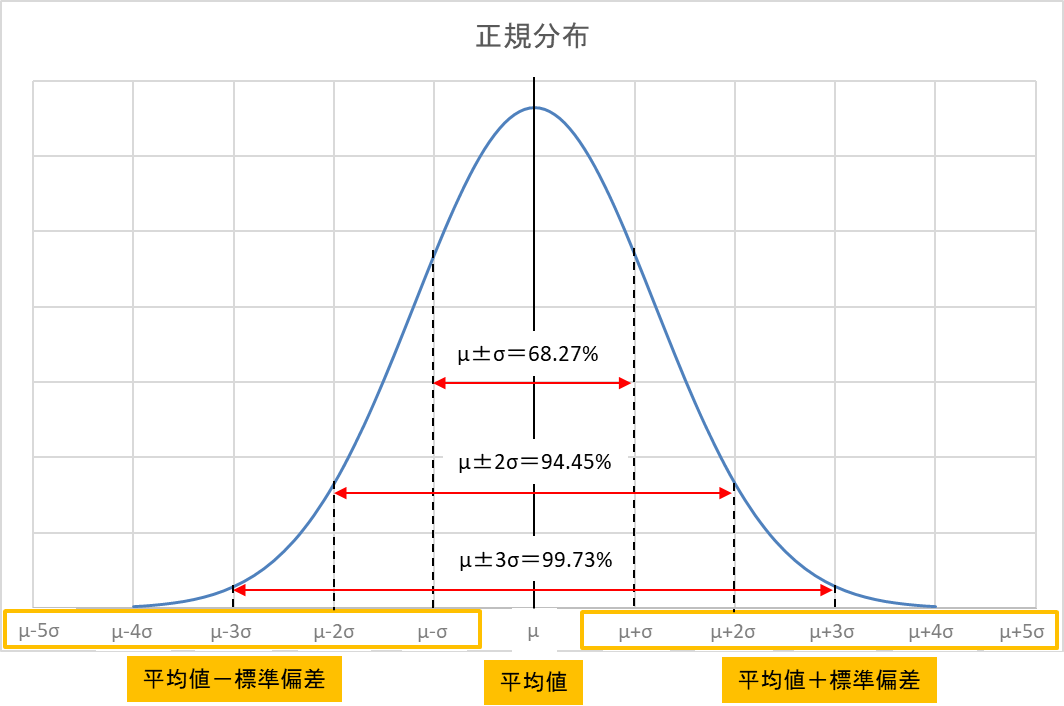
これを掘り下げて考えてみますと、、、
例えば、今後さらにデータを集めたとすると、集めたデータは68.27%の確率でμ±σの範囲に入る、94.45%の確率でμ±2σの範囲に入る、99.73%の確率でμ±3σの範囲に入る、と言う予測が立てられます。
これは、製品を作るうえでとても重要なことで、「製品のばらつきを確率で予測ができる」と言うことになるので「良否判定」や「精度の向上の改善」を判断する指標に使うことができます。
エクセルで標準偏差の計算をすると、計算誤差が大きくでる場合があります。これはエクセルの計算では有限桁数(桁がどこかで終わる)であるので、標準偏差の計算のように小数点以下の桁数が多い場合は数値を丸めて計算するので、真の値に対して誤差が発生します。別の方法としてはChatGPT(オープンAI)で計算することも可能です。何度か計算をさせてみたところエクセルとは違いかなり近い値が得られました。
正規分布(標準正規分布)
正規分布は平均値を基準にして前後にどれくらいばらついているかを表した釣り鐘形のグラフで、ばらつきの確率を標準偏差(σ)の値から求めることができます。
ばらつきの確率を求める計算は複雑なので、正規分布を標準化して標準正規分布(平均を0、分散を1としたブラフ)にすることで標準正規分布表(グラフの面積表)から確率を導きます。
正規分布と標準正規分布
変曲点とは曲線が上に凸から下に凸に切り替わるポイントのことで、正規分布の変曲点はσ(標準偏差)、標準正規分布は1となる
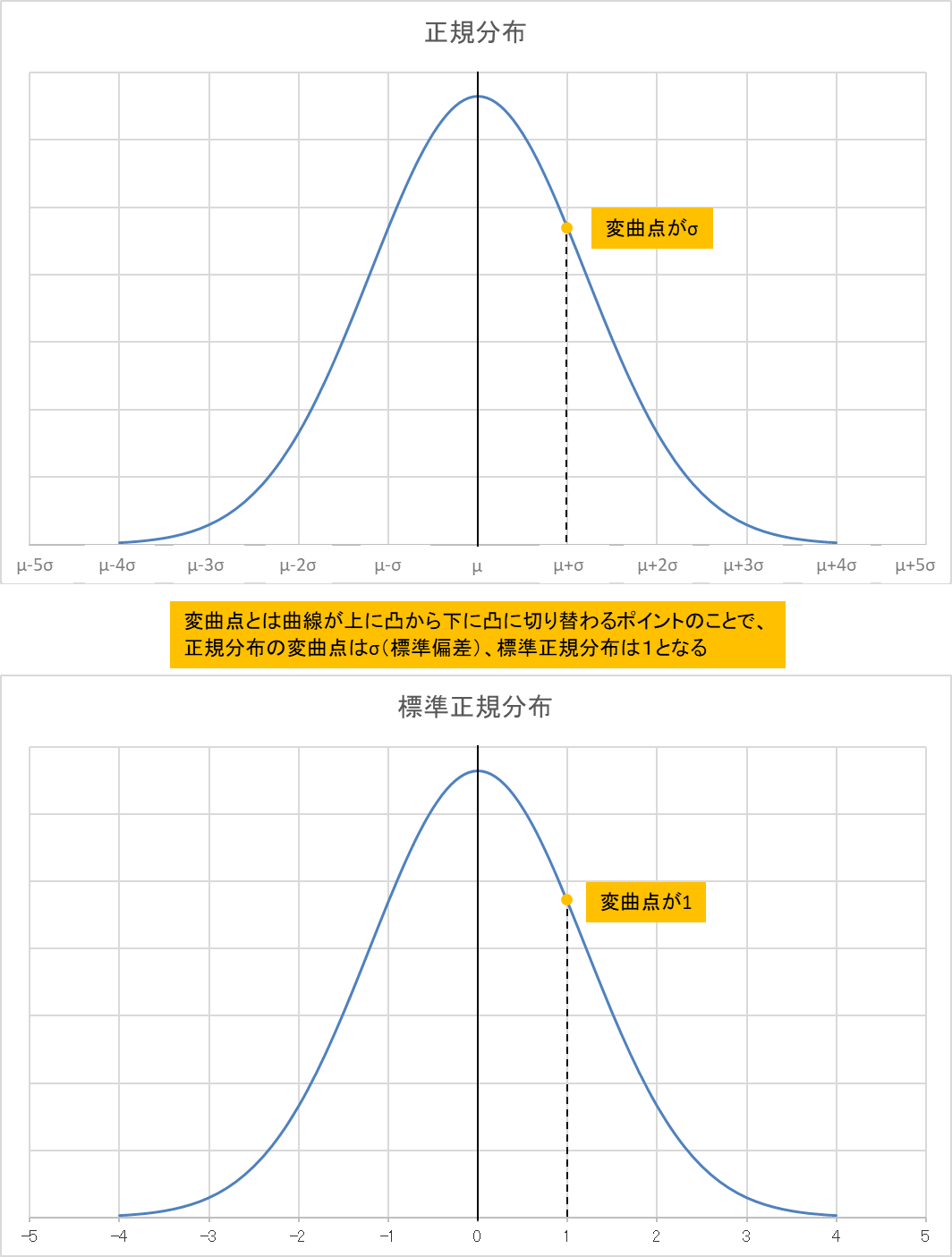
ざっくり言いますと、正規分布と標準正規分布はこんな感じで対応しています。
| 正規分布 | 標準正規分布 | 確率(%) |
| μ(平均値) | 0 | |
| μ+σ(標準偏差で求めた値) | 1 | 34.13(0から1の区間) |
| μ+2σ(2×標準偏差の値) | 2 | 47.72(0から2の区間) |
| μ+3σ(3×標準偏差の値) | 3 | 49.87(0から2の区間) |
| μ±1σ | ±1 | 68.27(0から±1の区間) |
| μ±2σ | ±2 | 95.45(0から±2の区間) |
| μ±3σ | ±3 | 99.73(0から±3の区間) |
*確率とは集めたデータの何%が指定した範囲に含まれているか?と言うことです。
これによって、集めたデータを正規分布から標準正規分布に変換して標準正規分布表に照らし合わせることで確率が分かるようになります。
標準正規分布表で確率を求めるためには正規分布を標準化する必要があって、具体的には標準偏差の値を標準正規分布の分散の値(表記はZ)に変換することです。
データの標準化のエクセル関数はコレです
-
=STANDARDIZE(x, 平均, 標準偏差) ・・・Xに標準化したい数値を指定する
この関数で分散の値(Z)がでますので、その値から標準正規分布表で確率を導くことができます。
例えば、「0からZの範囲」や「0±Zの範囲」や「0からZ以外の範囲」などに集めたデータの何%が含まれているのか?が分かるようになります。
*詳しくは下記の表を参照してください。
標準正規分布表
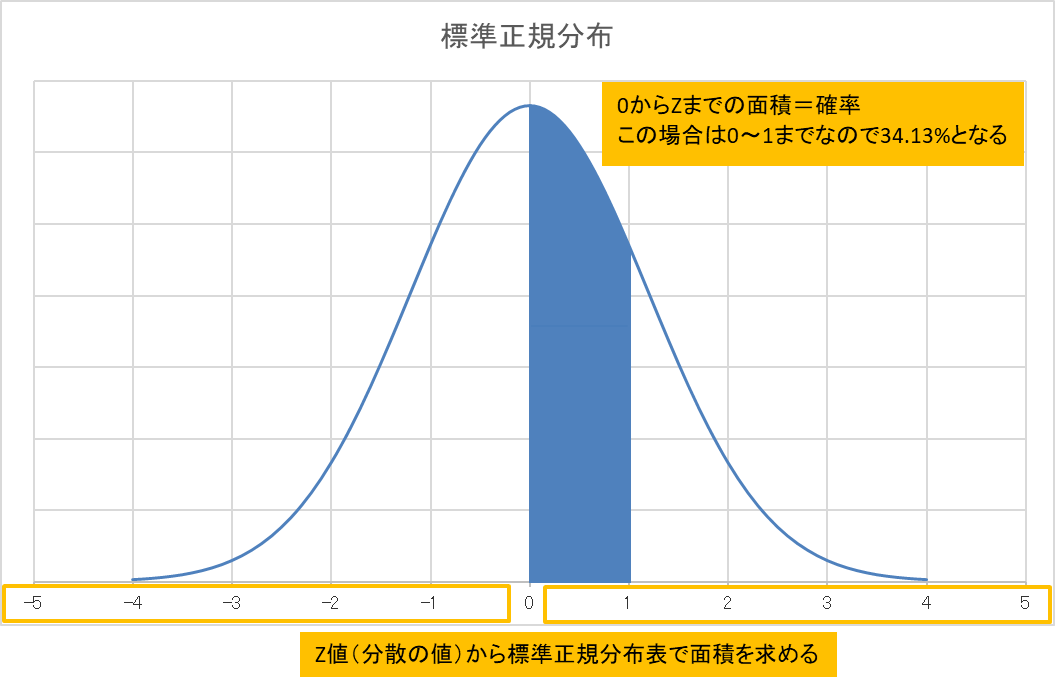
*標準正規分布表はグラフの面積を1としたときに、指定した範囲の面積がいくつなのか?を表しています。
*確率で考えるときは、下記の数値に×100をすると%の単位になります。
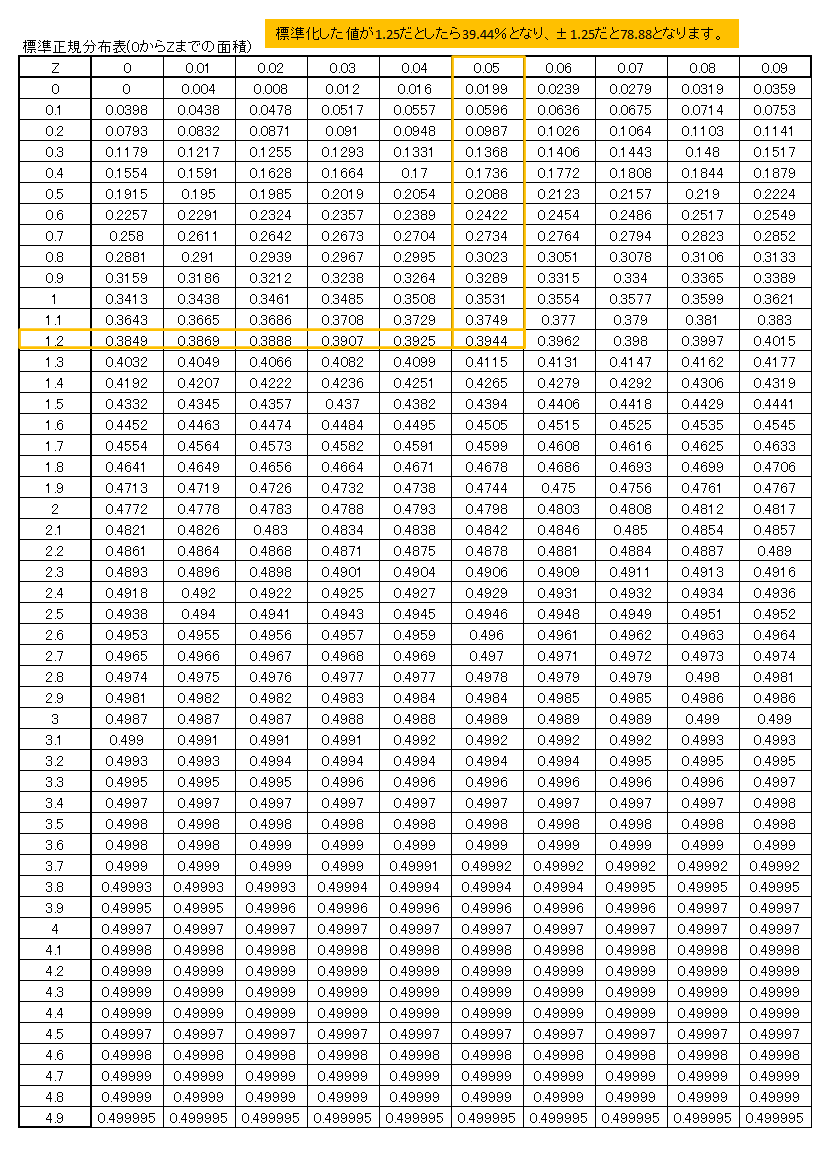
このように、集めたデータをもとに数値の確率が分かれば、「傾向」が分かるだけでなく「予測」や「異変の基準」の参考にもなります。これってかなり画期的なことではないでしょうか。
機械装置の評価と分析のポイントまとめ
それでは、機械装置の評価と分析について重要なポイントをまとめておきます。
ポイント
- 部品や組立の精度と機械装置の性能は数値がどれくらいばらつくのか?を分析して評価する
- 測定したデータを分析するためには、集めたデータをヒストグラムにしたとき一峰性であることが前提
- データは最低30回分測定する(N=30)
- データの分析は、最小値、最大値、平均値、標準偏差、正規分布などを総合的に判断しています
- 標準偏差と正規分布によって、データの確率が分かるようになる
以上5つのポイントです。
今回は私が行っているデータ分析の方法を紹介しましたが、分析の方法ややり方は様々だと思います。参考にしてください。
*統計学の入門におすすめな書籍はこちらです。初心者にも分かりやすい本です。
関連記事:【精度測定/精度調整】
以上です。

